Turing Machine Mastering the Foundations of Computation
Learn about the Turing machine, a crucial concept in computation. Dive into its definition, history, and impact on modern computing.
Few ideas in computer science have proven as groundbreaking as the Turing machine, developed by Alan Mathison Turing in 1936. No matter how complicated, this abstract tool with its unlimited tape and basic principles can replicate any computer program.
The Turing machine is the foundation of modern computational theory, not just a theoretical construct. It creates the theoretical limitations of what computers can do; hence, it bridges the gap between abstract mathematics and useful computing.
Grasping the foundations of computing and its restrictions depends on an awareness of the Turing machine.
Turing Machine: The Emergence of a Revolutionary Idea
Conceived by Alan Turing in 1936, the Turing machine was a theoretical construct predating contemporary computers. Designed to calculate every computable sequence, this simple but effective tool defined the bounds of computability.
Often considered the founder of computer science, British mathematician, logician, and computer scientist Alan Turing His efforts on the theoretical underpinnings of computing produced the Turing machine, a notion that would transform computation and mathematics.
“The Turing machine was a creation of Turing's attempt to solve the Entscheidungsproblem, a challenge posed by David Hilbert regarding the decidability of mathematical statements.”
In the annals of mathematics, 1936 was notable. While the development of the Turing computer arrived at a period when society was looking for solutions to basic difficulties, mathematicians were struggling with basic issues. The historical background emphasizes the issue in mathematics—known as the Entscheidungsproblem—that Turing's work tackled.
| Year | Event | Significance |
| 1936 | Publication of “On Computable Numbers” | Introduced the Turing machine, defining computability |
| 1936 | Turing's work on the Entscheidungsproblem | Addressed the decidability of mathematical statements |
The influence of the Turing machine was great, as it offered a computing paradigm and set the foundation for the creation of contemporary computers. The simplicity and grace of the Turing machine belie their importance in the annals of computing.
- A basic idea in computer science, the Turing machine shows the limits and force of computing.
- For mathematics and computer science, Turing's work in 1936 signaled a turning point.
Turing machine definition
Though it's almost ridiculous, imagine a machine so simple but the foundation of contemporary computers. Conceived by Alan Turing, the theoretical model known as the Turing machine has grown to form the basis of computer science. The Turing machine's outstanding potency comes from its simple elegance.
Based on a basic yet strong model with few main components, the Turing machine is It's like a bicycle: basic in form yet able to carry you great distances. A basic idea in the discipline: the Turing machine is beautiful in its capacity to compute everything that is computable.
“On Computable Numbers, with an Application to the Entscheidungsproblem,”
According to Alan Turing, the computer adheres to a set of guidelines and operates by reading and writing symbols on an infinite tape. The reason the Turing machine is so robust is its simplicity.
Three main parts comprise the Turing machine: a set of rules, a read/write head, and an endless tape. A The tape serves as the machine's memory, storing data in the form of symbols. Reading and writing these symbols falls to the read/write head; the set of rules controls the machine's behavior.
| Component | Description |
| Infinite Tape | It serves as the machine's memory, storing data in the form of symbols. |
| Read/Write Head | I am responsible for reading and writing symbols on the tape. |
| Set of Rules | Dictates the machine's actions based on the current state and symbol being read. |
The simplicity of the Turing machine belies its importance in the field of computing. Understanding its elements and their interactions helps us to better appreciate the basic character of computers.
Characteristics of a Turing Machine
Although the architecture of the Turing machine is shockingly simple, it is the key to understanding the limitations and possibilities of computing. Fundamentally, the Turing machine is a set of a few simple parts cooperating to process data.
The Infinite Tape: Unrestricted Memory
The Turing machine uses an infinite tape as its memory, providing an endless supply of readable and writable storage cells. Each concrete cell on this tape can carry a symbol from a limited alphabet. Crucially, the endless tape lets the Turing machine handle data without regard to a restricted memory capacity.
You'd You would never have to worry about running out of space for your vacation pictures, as your smartphone would have an unlimited capacity. The Turing machine is a strong theoretical model for computing, and its endless tape is akin to possessing limitless memory.
The Read/Write Head: Where the Enchantment Lives.
Another essential part of the Turing machine is the read/write head, which runs over the tape reading and writing symbols. One cell at a time, it advances precisely along the tape. Executing the instructions for computation on the Turing computer, the read/write head is its active constituent.
States and Transitions: The Decision-makers
The states and transitions of the Turing machine provide its “brainpower.” Depending on the current state and the symbol on the tape, the machine transitions between a limited number of states. A set of guidelines controlling the next state, the symbol to be written, and the direction in which the read/write head should travel shapes these transitions.
| Component | Function | Significance |
| Infinite Tape | Serves as memory, storing symbols | Provides unlimited storage for computation |
| Read/Write Head | Reads and writes symbols on the tape | Executes instructions, enabling computation |
| States and Transitions | Determine the machine's next action | Gives the Turing machine its computational power |
Understanding these elements and their interactions helps us grasp the basic ideas of computation that guide contemporary computer science.
Turing Machine: Formalism in Mathematics
Understanding the fundamental concepts of computing necessitates familiarity with the mathematical formalism of Turing machines. A pillar of computer science, this formalism offers a disciplined foundation for comprehending how Turing machines run.
Formal Definition: Q, Σ, δ and Friends
Usually expressed as a 7-tuple (Q, Σ, Γ, δ, q₀, B, F), this is the formal definition of a Turing machine. Q is a finite set of states; Σ is the input alphabet; Γ is the tape alphabet. Crucially, the transition function δ determines the actions of the machine depending on its present state and the symbol it reads.
One of the main ideas of this formalism is the notion of states and transitions. Fundamentally, the machine operates by changing its state based on the current state and the symbol read from the tape. The transition function translates the current state and symbol to the next state, writes the next symbol, and determines the direction of tape movement, thereby capturing this.
| Component | Description |
| Q | Finite set of states |
| Σ | Input alphabet |
| Γ | Tape alphabet |
| δ | Transition function |
| q₀ | Initial state |
| B | Blank symbol |
| F | Set of final states |
Changing roles: The Game's Rules
The central activity of a Turing machine is the transition function δ, which defines its movement from one state to another depending on the current state and the symbol it reads. This ability, a fundamental component of the Turing machine formalism, essentially functions as a collection of guidelines that control the machine's behavior.
Analyzing the transition function and its purpose in the operation of the Turing machine helps us understand its computing capacity as well as the mathematical ideas guiding it.
Turing Machines In Use
Rather than merely theoretical ideas, Turing machines provide a glimpse into the basic essence of computing. Examining their behavior helps us better understand the basic structure of computation.
Easy Exercises to Help You Understand
Let's start with a straightforward example that showcases the capabilities of a Turing machine. Think of a machine assigned a simple arithmetic task—addition, for example. Like a hesitant consumer at a supermarket, the machine moves back and forth along its tape, following a program that ultimately generates the correct total. Though seeming little, this method shows how easily the machine can run computation using a set of simple processes.
Further examination reveals that Turing computers reduce even complex calculations to smaller, repetitive tasks. The complexity of Turing computers is as much a source of beauty as their power. They show that with the correct software, a computer can do wonderful feats via tenacity and accuracy.
Step-by-Step Visualization of Computation
Observing a Turing machine in action step-by-step provides a deeper understanding of its operation. The machine reads and writes symbols on its tape, following a predefined series of states and transitions. This procedure methodically, if not excitingly, transforms input into output. Though the consequences are great, seeing this process is like seeing paint dry.
One can observe how a Turing computer meticulously carries out its program by adhering to its execution sequence, which in turn modifies the symbols on the tape to achieve the desired outcome. This technique shows not just the processing power of the computer but also its elegant design.
Turing Machine: The Authority of Computing
Though their simplicity defines their power, Turing machines can compute anything that is “effectively calculable.”
Understanding the limitations and possibilities of computing has always depended primarily on Turing machines. They provide a basic paradigm for computation capability.
What can Turing machines compute?
From simple arithmetic to sophisticated algorithms, there are many uses for Turing machines. Their capacity to read, write, and control symbols on an endless tape forms the foundation of this skill.
| Capability | Description |
| Arithmetic Operations | Perform basic arithmetic like addition and subtraction. |
| Complex Algorithms | Execute intricate algorithms involving multiple steps and decisions. |
The Bold Claim Made by the Church-Turing Thesis
According to the Church-Turing thesis, a Turing computer can calculate every basically calculable function. “We may compare a man in the process of computing a real number to a machine that is only capable of a finite number of conditions,” Alan Turing once pointed out. This argument underlines the universality of the machine.
“We could contrast a man calculating a real number with a machine limited to a finite number of conditions.” Alan Turing:
This thesis suggests that Turing machines are the ultimate limit of computability, therefore implying significant consequences for the discipline of computer science.
Constructing More intricate Turing machines
Deeper exploration of the universe of Turing machines reveals that their simplicity hides their capability for complexity. Combining simple Turing machines will enable us to create more advanced devices capable of handling a broad spectrum of computing chores.
Addition and Mathematical Operations
Turing machines can perform arithmetic operations such as addition, subtraction, multiplication, and division by following a sequence of steps that involve reading and writing on the tape. A Turing machine may be built, for instance, to add two integers by reading the numbers shown on the tape, doing the required computations between states, and then writing the result back onto the tape.
The following is a condensed summary of how a Turing machine may add:
- Consult the first number shown on the cassette.
- Change to a state that marks the beginning of the adding procedure.
- Reading the second number requires moving down the tape.
- Add tape manipulation guided by pre-defined guidelines.
- Record the outcome back on the tape.
Pattern Recognition and String Manipulation
Turing machines are also capable of manipulating strings and recognizing patterns, which involve intricate series of state transitions. For example, to change a string from “hello” to “goodbye,” a Turing Machine must read the input string, navigate through numerous stages according to its program, and then record the output string onto a tape.
Human innate ability to detect patterns becomes a complex series of actions for a Turing machine. When expressed computationally, this process emphasizes the subtle complexity behind apparently straightforward human chores.
Implementing difficult algorithms into simpler Turing machine instructions can help us better grasp the underlying computer job execution. This procedure is like breaking apart a recipe into its fundamental components: a computing job calls for certain instructions and data manipulation, just as a gourmet dish calls for particular ingredients and cooking techniques.
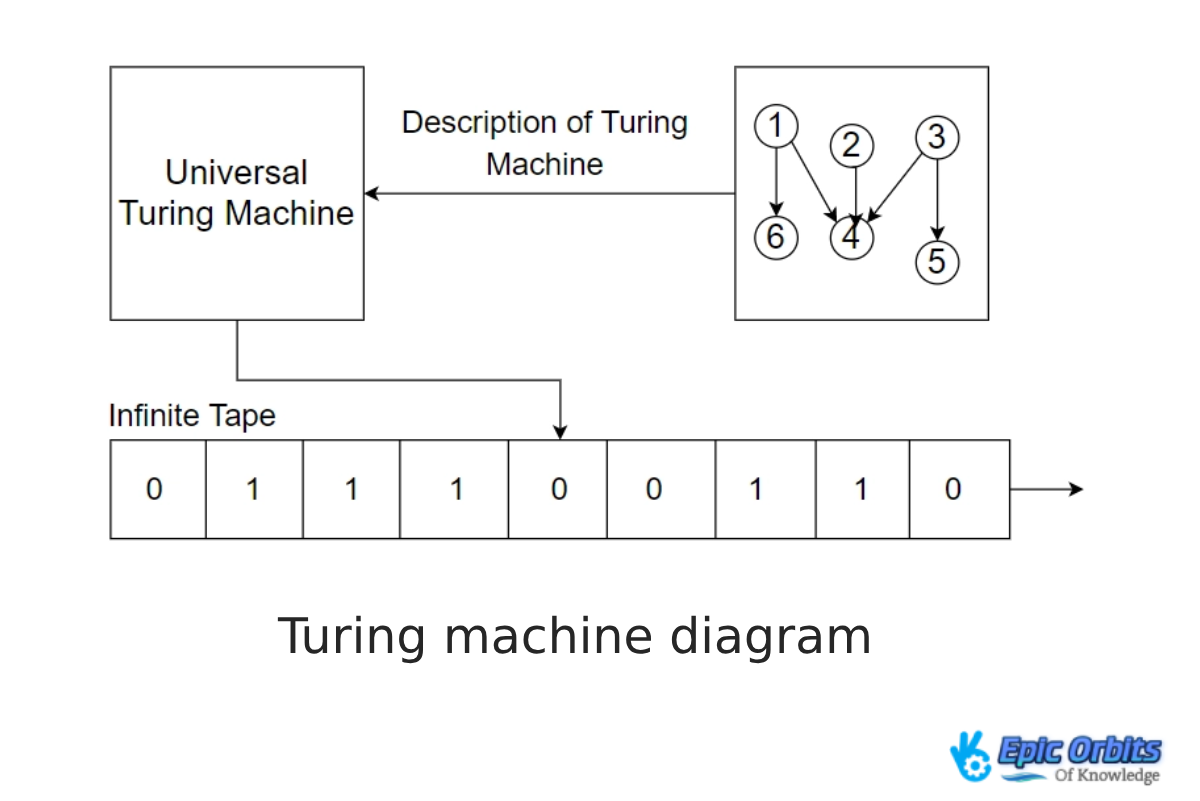
The Universal Turing Tool
The Universal Turing Machine is so adaptable that it can replicate the actions of any other machine. Conceived by Alan Turing, this theoretical tool transformed the idea of computing by proving that every calculation any other Turing machine could potentially accomplish could be accomplished by one machine.
TT The Universal Turing Machine, not just a conceptual creation, serves as the foundation for contemporary computing. It practically became the forerunner of the stored-program computer due to its ability to read and execute the descriptions of other devices.
Another Machine Simulation Machine
The genius of the Universal Turing Machine lies in its ability to replicate the behavior of any other Turing machine. Therefore, the Universal Turing A machine is capable of reading the description of any other Turing machine and then replicating its behavior using a given input. This feature enhances the potency of the theory of computation.
| Machine Type | Capability | Universal Turing Machine Equivalent |
| Turing Machine | Specific Computation | Simulated by Universal Turing Machine |
| Universal Turing Machine | Any Computation | Self-Simulation |
| Modern Computer | Varied Tasks | Conceptual Foundation |
Modern Computer's Blueprint
Modern computers sprang from the ideas of the Universal Turing Machine. Separating the “program” (instructions) from the “data” (input) created a basic idea that still drives computer architecture today. Revolutionary in 1936, this difference made it possible to build flexible machines capable of programming for a range of activities, from basic computations to sophisticated simulations.
T The Universal Turing Machine has significantly influenced the development of practical computers and programming languages, thereby surpassing the realm of theoretical computer science. As we use computers for various purposes today, we are drawing on the conceptual basis set by Turing's Universal Machine.
Variants of the Turing Machine
The simplicity of the Turing machine hides the diversity of its variants; it is designed to maximize performance and expand its range of action. Although the fundamental concept is strong, academics have investigated changes to improve its efficiency and adaptability in other computing environments.
Turing Machine: Multi-tape machines
One notable variant is the multi-tape Turing computer, which uses many tapes to handle data. This architecture enables more effective processing by employing many tapes at various stages of the computing process. Though more efficient, multi-tape computers do not have greater computational power than the original single-tape Turing machine.
Non-deterministic Turing machines
Another variant is non-deterministic Turing computers, which allow the machine to simultaneously explore multiple processing While this paradigm may simplify algorithm creation in certain situations, it does not expand the range of computable functions beyond those achievable by deterministic Turing computers.
Quantum Turing Machine
Quantum TuRing machines use quantum mechanical concepts to perform calculations These devices can process enormous volumes of data in parallel using qubits, potentially solving certain problems more quickly than conventional Turing computers. Until then, the fundamental constraint of computability remains unchanged.
These variants, which include multi-tape, non-deterministic, and quantum Turing machines, demonstrate the adaptability and depth of the Turing machine paradigm. They underline how, even if they do not exceed the computing capability of the original model, various computational techniques might provide benefits in efficiency and application.
Turing Machine: The Restraints of Calculating
Investigating Turing machines reveals the intriguing and intricate universe of computational constraints. Although Turing machines can replicate any algorithmic process, certain issues fall beyond their purview.
The Halting Problem: What Can't Computers Do?
The halting problem of Turing machines is among their most significant limitations. First noticed by Alan Turing, this question concerns whether it is feasible to ascertain, from an arbitrary program and input, whether the program will finally stop or continue indefinitely. Turing demonstrated a basic limit to computing via a clever argument showing that no algorithm can solve this issue for all conceivable programs.
People often liken the stopping issue to the question of whether a phrase can ever finish. This topic challenges the basic essence of computability and draws attention to the fact that any computer cannot solve certain problems by nature.
| Problem Type | Computability | Example |
| Decidable | Solvable by a Turing Machine | Determining if a number is prime |
| Undecidable | Not solvable by a Turing Machine | The halting problem |
Undecidable Problems: Outreach of Algorithms Beyond Reach
In addition to the halting problem, there are numerous intractable problems that current methods cannot resolve. In certain formal systems, the truthfulness of these mathematical problems remains unknown, rendering them unresolvable.
Knowing these limits is essential, as it helps us to see that they are basic limits of computation itself, not defects in our computing models. Undecidable questions hold significant implications for mathematics and computer science, suggesting that certain facts should remain perpetually beyond our algorithmic grasp.
“My language's limits are those of my world.” Ludwig Wittgenstein
Tractatus Logico-Philosophicus Ludwig Wittgenstein
This philosophical viewpoint emphasizes the need to realize the limitations of computing, as shown by the research of Turing machines and the unsolved difficulties.
Modern Computing and Turing Machine
The Turing machine, a theoretical model that has shaped the digital landscape, primarily drives modern computing. As a basic mathematical notion, this fundamental principle in computer science has developed into the intricate silicon chips running modern appliances.
Turing Machine: From Silicon Reality to Theoretical Model
The path from Turing's theoretical model to the silicon reality of contemporary computers demonstrates human creativity. Through its abstract character, the Turing machine set the foundation for the creation of actual computers. In terms of computational capability, modern computers—with their complex interfaces and rapid processing capacity—are essentially identical to Turing's initial machine. Their speed and the data storage media—no more paper tape—define their main variations.
- The development of computers theoretically transformed Turing's concept into the cornerstone of modern technology.
- Modern computers nevertheless have their roots in the ideas expressed by Turing, notwithstanding developments.
Computational Complexity: Beyond P, NP
Deeply anchored in Turing's work, computational complexity theory sorts problems according to solvability and efficiency. P-classified problems are said to be tractable; NP-hard problems provide great difficulty. With significant ramifications for cryptography, optimization, and many other fields of computer science, the P vs. NP dilemma is still a fundamental unresolved subject.
Knowing the boundaries of computing as specified by Turing machines still directs computer science research. Turing's theoretical underpinnings limit what is feasible and motivate fresh ideas to difficult challenges.
- The theory of computational complexity clarifies the algorithm's efficiency.
- A basic hurdle in theoretical computer science is the P vs. NP issue.
Turing Machine: Several Computational Models
Beyond the basic function of the Turing machine, other models of computation have greatly expanded our knowledge of what computing is all about. Although their methods vary, all models finally agree on the same computational capacity as Turing machines, therefore highlighting the stability of the theory of computation.
Lambda Calculus: Computed Using Functions
Alonzo Church's development of lambda calculus offers a very distinct method of computing. It chooses a function-based paradigm over a machine-based one, such as those based on Turing machines. Lambda calculus demonstrates the adaptability of the computational idea by use of functions applied to inputs, therefore facilitating computing.
Recursive Functions: Another Computable Route
By emphasizing the recursive division of issues into smaller subproblems, recursive functions provide yet another viewpoint on computing. Inspired by mathematical recursion, this method shows how iteratively applying functions may provide computability, hence reflecting the Russian nesting doll effect but with mathematical accuracy.
Cellular automaton: pattern-based computing
A more visually oriented type of computing, cellular automata are where basic principles applied to grid cells produce intricate patterns. Underlining the complex beauty of computational systems, this model shows how computing may arise from the interplay of basic components under simple principles.
It is a wonderful realization that these many models have computational capability equivalent to that of Turing computers. It implies that the more abstract nature of computing is quite independent of any one paradigm or representation.
| Model | Description | Key Feature |
| Lambda Calculus | Computation through function application | Function abstraction |
| Recursive Functions | Problem-solving through recursion | Recursive definition |
| Cellular Automata | Pattern generation through simple rules | Local interaction |
| Turing Machines | Symbol manipulation on an infinite tape | Read/write head |
These diverse models show the depth of computational theory and provide many prisms through which one may grasp the essence of computing. Investigating these models helps us to better respect the basic ideas guiding all computer systems.
Philosophical Conventions of Turing Devices
Turing's work on computation has spurred discussions on the core of the human mind and machine intelligence; therefore, it transcends the field of computer science. We start to wonder about the fundamental nature of intelligence and awareness as we investigate the powers and constraints of Turing machines.
Computers, Minds, and the Turing Test
Proposed by Alan Turing, the Turing Test gauges a machine's capability for cognition by suggesting that it be able to show intelligent conduct either matching or indistinguishable from that of a person. Discussions on artificial intelligence have revolved mostly around this test, which begs issues regarding the standards for proving whether robots can really have consciousness.
The Turing Test avoids the difficulties of precisely defining consciousness or intelligence by emphasizing the machine's capacity to replicate human discourse. Rather, it presents a sensible method for evaluating a computer's intelligent behavior; hence, it generates discussion on whether such a proof is adequate to assert that a machine is “thinking.”
Artificial intelligence: can machines think?
Turing's concepts have greatly influenced the evolution of artificial intelligence (AI). Although they are not exactly meant to replicate human brain processes, modern artificial intelligence systems have proven very skilled at handling enormous volumes of data to reach certain objectives. This raises philosophical questions about the nature of computing and consciousness, as well as whether the human mind can be considered a sophisticated Turing machine operating on biological “wetware.”
A great philosophical investigation is a reflection on whether awareness might arise from computing. It draws on our knowledge of the human mind and how it relates to the machinery we create. Theoretically, Turing's work still shapes these discussions by showing how far-reaching abstract mathematical ideas may be for our knowledge of intelligence, awareness, and the possibilities of computers.
Conclusion
The simplicity and grace of the Turing Machine hide its enormous impact on computer science. Alan Turing's clever concept of computing, which transforms the abstract into the concrete, has permanently changed modern technology.
When one considers the remarkable path from Turing's abstract mathematical model to the digital revolution, one finds that the Turing Machine was more than simply a theoretical construct. It was a roadmap for the contemporary computers that pervade every part of our lives.
Apart from addressing a particular mathematical challenge, Turing's work formed the theoretical underpinnings of computer science, therefore defining both the capabilities and, essentially, limitations of computers. Our knowledge of computing reminds us that certain issues remain permanently beyond algorithmic solutions, as Turing revealed, including the halting problem that shapes us.
With its unlimited tape and set of rules, the Turing Machine evolved into the conceptual design for gadgets that now fit in our pockets and link billions of people globally—a change Turing himself could barely have envisioned. Even as we push the limits of quantum computing, artificial intelligence, and other modern technology, we continue to operate within the basic framework that Turing built.
This continuing legacy emphasizes how timelessly relevant Turing's vision is. Still fundamental in the area, the Turing Machine shapes the next generations of academics and engineers. The ideas set out by Turing will be absolutely vital as we keep innovating, leading us across the complexity of contemporary computers and Turing machines.
